La prova di trazione: relazioni "reali" tra tensione e deformazione

relazione “reale” tra tensione e deformazione

Lo studio di figura 1 rivela che se un materiale è allungato molto oltre la sua massima deformazione elastica (20 o 30 volte), la tensione “nominale” (ne abbiamo parlato in altro articolo) diventa fittizia, perché si basa su un’area di sezione significativamente diversa da quella effettiva.

Relazione a valori nominali Tensione-Deformazione per acciaio laminato a caldo 1020 — Figura 1. Relazione a valori nominali Tensione-Deformazione per acciaio 1020 laminato a caldo. Scala lineare.

In questi casi tale limitazione può essere evitata calcolando la tensione “reale”, qui denominata $\sigma _{T}$ , e definita come il rapporto tra il carico e l’area della sezione esistente quando il carico agisce.

Dunque, $\sigma = \frac{P}{A_{0}}$ e $\sigma_{T} = \frac{P}{A_{f}}$ , ove i pedici 0 ed f indicano rispettivamente il valore iniziale e finale della sezione e P indica il carico.

Dato che vale la relazione $A_{f}=\frac{A_{0}}{1+\varepsilon }$ e sostituendo nella definizione precedente, si ottiene:

$\sigma _{T}=\frac{P}{A_{0}}\times (1+\varepsilon )=\sigma \times (1+\varepsilon )=\sigma R$

dove si è indicato:

$R=\frac{A_{0}}{A_{f}}=1+\varepsilon$

Se alla luce di quanto detto andassimo a ricalcolare i valori (a stress nominale) B,C ed F, indicati nella figura, a tensioni reali, otterremmo:

B=39 x 1=39; C=66 x 1,3=86; 45 x 2,5=113 ksi

Notare che la tensione reale aumenta continuamente fino al punto di rottura.

In modo simile, l’uso della deformazione nominale non è adatto quando sono coinvolte grandi deformazioni. In questo caso sarebbe più indicato l’uso della deformazione reale $\varepsilon _{T}$ .

Consideriamo ad esempio un campione di materiale duttile, di lunghezza unitaria, che venga allungato prima di 5 volte rispetto al valore nominale e poi successivamente fino a 5,1 volte rispetto al valore nominale.

All’allungamento finale di 0,1 (da 5 a 5,1 volte il valore iniziale), corrisponderebbe un allungamento nominale di $\frac{0.1}{1}=0.1$ mentre l’allungamento reale sarebbe di molto inferiore e pari a $\frac{0.1}{5}=0.02$ (variazione di lunghezza diviso la lunghezza del campione all’istante precedente l’ultimo allungamento).

Matematicamente, la deformazione reale può essere definita come:

$\varepsilon _{T}=\sum_{L_{0}}^{L_{f}}\frac{\Delta L}{L}=\int_{L_{0}}^{L_{f}}\frac{dL}{L}=\ln R=\ln (1+\varepsilon )$

ove i pedici 0 ed f rappresentano la lunghezza iniziale e quella finale. Per i metalli le differenze tra deformazioni nominali e reali sono trascurabili se la deformazione non supera di diverse volte la massima deformazione elastica.

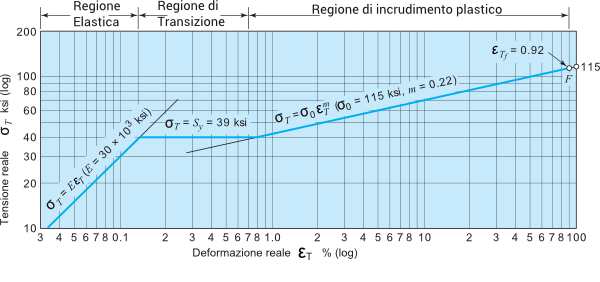
Figura 2. Relazione a valori reali Tensione-Deformazione per acciaio 1020 laminato a caldo.

La figura 2, partendo dagli stessi dati di figura 1, illustra le relazioni reali tensione-deformazione. Dal grafico si possono dedurre relazioni generali riguardanti l’effetto dell’incrudimento (cold working) sulla resistenza dei metalli. Lo studio delle 3 regioni individuate nel grafico, poi, ci rivela alcuni importanti concetti.

La regione elastica. A stretto rigore, il modulo di Young è il rapporto tra tensione nominale ed estensione nominale, ma con errore trascurabile esso è anche il rapporto tra gli analoghi valori reali.
Dunque:

$\sigma _{T}=E\varepsilon _{T}$

Dove E=modulo di Young. Nel grafico di figura 2, in coordinate logaritmiche, questa equazione corrisponde ad una retta di pendenza unitaria passante per il punto 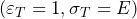$(\varepsilon _{T}=1,\sigma _{T}=E)$ . E si può dunque anche interpretare come il valore di tensione necessario a produrre una deformazione elastica unitaria.
La regione di incrudimento plastico.
A questa regione corrisponde l’equazione:

$\sigma _{T}=\sigma _{0}\varepsilon _{T}^{m}$

Si nota che questa equazione ha la stessa forma di quella precedente, fatta eccezione per l’esponente

m= indice della tendenza a incrudimento per deformazione plastica a freddo= pendenza della retta in coordinate logaritmiche.

La costante $\sigma _{0}$ è analoga alla costante di proporzionalità elastica E in quanto essa rappresenta lo stress reale che produrrebbe una deformazione reale unitaria.
La regione di transizione. Per un materiale ideale il limite elastico (approssimativamente uguale alla tensione di snervamento) corrisponderebbe alla intersezione delle linee di comportamento plastico ed elastico. In realtà i materiali reali hanno valori di $S_{e}$
più alti o più bassi, rendendo quindi necessaria la definizione empirica di una curva di transizione.

Bisogna sottolineare il fatto che i dati relativi all’incrudimento dei materiali da costruzione non sono facilmente disponibili. Qui sotto una tabella con i valori tipici per alcuni metalli.

Articoli correlati